Graphiques de trigonométrie avec Octave

Octave est une plateforme de calcul scientifique libre et gratuite. Elle est particulièrement adaptée aux opérations mathématiques et dispose d'un mécanisme simple pour tracer les données. Les visualisations de trigonométrie sont particulièrement puissantes avec Octave. Cet article traite de la façon de tracer des visualisations de trigonométrie avec Octave.

À propos d'Octave

Le développement d'Octave a été lancé en 1992 par John W. Eaton. Il est en grande partie écrit en C++ et contient un interprète du langage de script de haut niveau Octave.

Le langage Octave est principalement compatible avec Matlab. Sa syntaxe est la suivante matricielle et supporte diverses structures de données et permet même la programmation orientée objet (OOP).

Octave peut être exécuté en ligne de commande, mais dispose également d'une interface utilisateur graphique (GUI).

Fonctions trigonométriques en Octave

L'Octave couvre un grand nombre de fonctions trigonométriques. La plupart des fonctions marchent avec des radians. Mais un certain nombre de fonctions marchent aussi directement avec les degrés. Si vous voulez convertir des degrés en radians, vous pouvez multiplier les degrés par pi/180.

Ainsi :

radian = degree * pi/180

Une liste de toutes les fonctions trigonométriques utilisables est disponible à l'adresse du site web d'Octave.

Tracer le sinus

Pour le rendre plus intéressant, ce script simple trace à la fois le sin(x) et le sin(x*3) dans le même graphique.

Pour distinguer l'un de l'autre, j'utilise la couleur noire pour sin(x) et rouge pour sin(x*3).

Voici le script Octave que vous pouvez entrer dans l'éditeur ou exécuter dans la ligne de commande Octave :

sine.m

x = -10:0.1:10;
plot (x, sin(x), 'k', x, sin(x*3), 'r')

X définit la plage des valeurs du graphique, de -10 à 10.

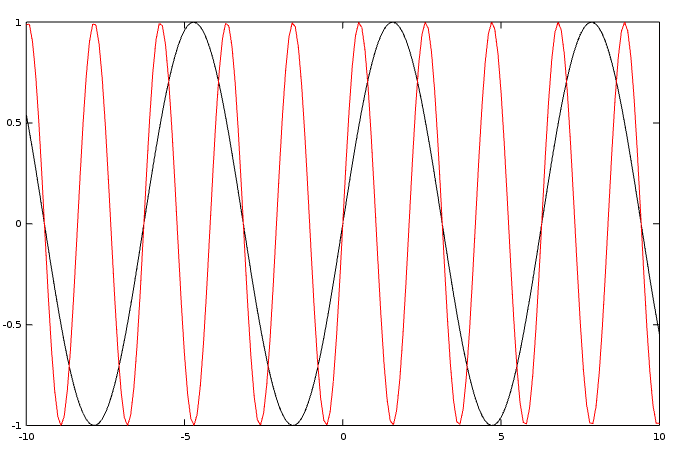
Dans le graphique, vous pouvez voir que le sin(x*3) a trois fois la fréquence du sin(x). Il est plus dense.

Tracer le sinus et le cosinus

Nous pouvons également combiner une fonction sinus et cosinus en un seul graphique. Vous pouvez ainsi voir clairement la différence entre les deux fonctions.

cosine.m

x = -10:0.1:10;
plot (x, sin(x), 'k', x, cos(x), 'b')

Dans ce cas, la fonction sinusoïdale est noire et la fonction cosinusoïdale est peinte en bleu.

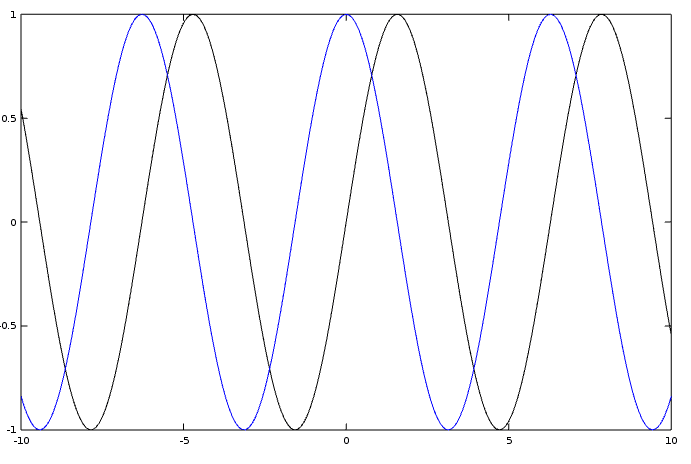
Tracer la tangente

Une autre fonction intéressante à représenter graphiquement est la fonction tangente. La tangente est le rapport entre le sinus et le cosinus.

Le seul problème avec cette fonction est lorsque le cosinus devient nul, car on ne peut pas le diviser par zéro. Ainsi, chaque fois que le cosinus devient nul, il est indiqué par des asymptotes.

L'Octave nous permet également d'ajouter un titre et des descriptions pour les axes x et y. Ceux-ci sont ajoutés dans le script ci-dessous :

tan-1.m

x = -10:0.1:10;
plot (x, tan(x), '--')
title('Tangent')
xlabel('x')
ylabel('tan(x)')

Le tracé de la tangente est en pointillés, ce qui est dû au troisième paramètre de la fonction de tracé ("- -").

Faites attention à ne pas appeler votre nom de fichier de script de la même façon qu'une fonction d'Octave, car vous obtiendriez alors une erreur.

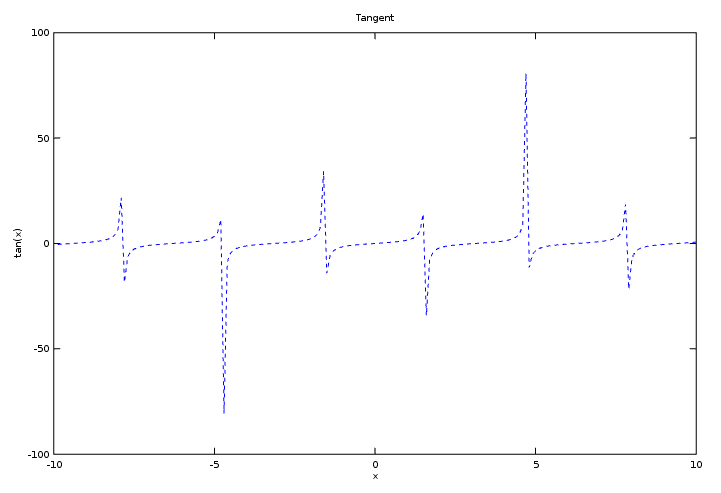
Conclusion

Il n'est pas difficile d'écrire ces petits scripts Octave pour représenter graphiquement des fonctions trigonométriques. J'espère que cet article vous a inspiré et que vous commencez à explorer les merveilles des mathématiques par vous-même.

Références

• Octave : https://www.gnu.org/software/octave